On traite le cas du nœud dans sa plus grande généralité. Un nœud peut être constitué :

• d’un casier ;
• de prises avec débits entrants ou sortants ;
• de biefs confluents ou défluents.

Les concepts et variables intervenant au nœud sont résumés dans le schéma suivant (seules les classes de qualité dérivantes sont considérées) :

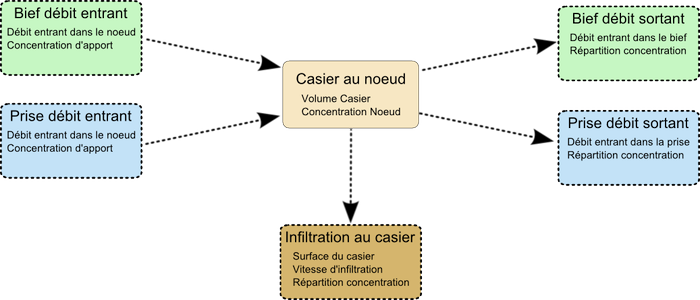
Un casier est connu sous la forme d’une suite monotone
de couples (surface, cote). Ce casier peut être soumis à
l’évaporation connue sous la forme
d’une vitesse d’évaporation
$V_{ep}(t)$ et à une vitesse d’infiltration sous la forme $v_{inf}(Z_{nd})$,
$Z_{nd}$ étant la cote dans le casier.

Le Nœud reçoit ou perd du débit via les prises
($Q_p$) et les biefs ($Q_b$). Les débits entrants dans le nœud sont positifs, et les sortants négatifs.

Les biefs sont identifiés par un sens d’écoulement lié
à leur topologie. Ce sens « topologique » d’écoulement
est invariable dans le temps :

• $s_{b}=1$ pour les biefs confluents
• $s_{b}=-1$ pour les biefs défluents

Le débit $Q_b$ est
positif s’il coule dans le sens
d’écoulement du bief et négatif s’il
coule dans le sens inverse. On obtient le débit entrant ou sortant du
nœud avec le bon signe par la formule : $s_{b}Q_{b}$

Débits entrants dans le nœud (i.e. débits positifs)

Pour les biefs confluents ou défluents avec , $s_{b}Q_{b}>0$ ou les
prises avec $Q_{p}>0$ , on a une condition limite
$C$ qui est la concentration d’apport dans le nœud.

Débits sortants du nœud (i.e. débits négatifs)

Biefs

Pour les biefs confluents ou défluents avec , $s_{b}Q_{b}<0$ , on a
$C_{b}=k_{b}C_{nd}$ .

Prises

Pour les prises avec $Q_{p}<0$ , on a $C_{p}=k_{p}C_{nd}$.

Infiltration au nœud

On a $C_{\mathit{inf}}=k_{\mathit{inf}}C_{\mathit{nd}}$ et
$Q_{\mathit{inf}}=S_{\mathit{cas}}v_{\mathit{inf}}$ avec :
$S_{cas}$ la surface
du casier, $v_{inf}$
la vitesse d’infiltration,
$C_{\mathit{nd}}$ la
concentration au Nœud.

Débits de stockage au casier

On considère le casier comme un bassin à connexion directe au noeud,
la concentration du noeud est donc la même que celle du casier. La
quantité de matière présente dans le noeud-casier est :
$m_{\mathit{Cas}}=V_{\mathit{Cas}}C_{\mathit{nd}}$ et le débit entrant
ou sortant du noeud s’obtient avec :
$Q_{\mathit{cas}}=S_{\mathit{cas}}\frac{\mathit{dZ}_{\mathit{nd}}}{\mathit{dt}}$.

Équation du bilan de masse au nœud

Écrivons l’équation de conservation de la masse
d’une classe de qualité au nœud $m_{\mathit{nd}}$
à l’instant t du calcul en tenant
compte d’un terme source au nœud.

Au temps t on connaît :

• la surface $S_{cas}$ du casier, son volume $V_{cas}$ ainsi que
  sa cote $Z_{nd}$,
• les débits entrants et sortants du nœud,
• les concentrations d’apport liées aux débits entrants dans le nœud,
• les coefficients de répartition liés aux débits sortants du nœud.

$\frac{\mathit{dm}_{\mathit{nd}}}{\mathit{dt}}=\sum_{s_{b}Q_{b}>0}C_{b}s_{b}Q_{b}+\sum_{s_{b}Q_{b}<0}k_{b}s_{b}Q_{b}C_{\mathit{nd}}$
$+\sum_{Q_{p}>0}C_{p}Q_{p}+\sum_{Q_{p}<0}k_{p}Q_{p}C_{\mathit{nd}}-k_{\mathit{inf}}S_{\mathit{cas}}C_{\mathit{nd}}v_{\mathit{inf}}+V_{\mathit{Cas}}E(t,C_{\mathit{nd}})$

Avec $\frac{\mathit{dm}_{\mathit{nd}}}{\mathit{dt}}=\frac{d\left(C_{\mathit{nd}}V_{\mathit{cas}}\right)}{\mathit{dt}}=\frac{dV_{\mathit{cas}}}{\mathit{dt}}C_{\mathit{nd}}+\frac{dC_{\mathit{nd}}}{\mathit{dt}}V_{\mathit{cas}}$,
l’équation de conservation de la masse au nœud devient :

$\sum _{s_{b}Q_{b}>0}C_{b}s_{b}Q_{b}+\sum _{Q_{p}>0}C_{p}Q_{p}+V_{\mathit{Cas}}\left(E(t,C_{\mathit{nd}})-\frac{\mathit{dC}_{\mathit{nd}}}{\mathit{dt}}\right)$
$+C_{\mathit{nd}}\left[\sum _{s_{b}Q_{b}<0}k_{b}s_{b}Q_{b}+\sum _{Q_{p}<0}k_{p}Q_{p}-k_{\mathit{inf}}S_{\mathit{cas}}v_{\mathit{inf}}-\frac{\mathit{dV}_{\mathit{cas}}}{\mathit{dt}}\right]=0$

Contraintes au nœud pour les k

3 cas sont envisageables pour les coefficients de répartition de concentration sur les départ de matière du nœud :

Tous les départs sont homogènes

Tous les k valent alors 1 : la conservation de la masse au nœud est assurée par l’équation de conservation de la masse au nœud quelque soit les variations de débits et de concentration.

Les départs sont hétérogènes et il y a un casier au nœud

La masse de polluant entrant ou sortant du casier assure la conservation de la masse au nœud en permanent et en transitoire.

Les départs sont hétérogènes et il n’y a pas de casier au nœud

Il faut ajuster la valeur d’au moins un coefficient de répartition pour assurer la continuité au nœud avec la contrainte que ce coefficient reste positif.

L’utilisateur défini les coefficients de répartition aux prises, au bief et à l’infiltration. Pour chacun de ces coefficients, il définit aussi si ceux-ci sont fixes ou ajustable pour assurer la continuité au nœud (Sauf pour l’infiltration car elle n’a lieu que dans un nœud avec casier et il n’y a donc pas d’ajustement dans ce cas).

La continuité s’effectue en introduisant un coefficient
d’ajustement $k_{a}$ tel que chaque coefficient de répartition puisse s’écrire
ainsi : ${k_{a}}^{b_{i}}k_{i}$ où $b_{i}$ est le choix pour le
coefficient $k_{i}$ entre rester fixe $b_{i}=0$ et être ajustable
$b_{i}=1$ pour assurer la conservation de la masse. De ce fait, les
deux possibilités sont représentées de cette façon :

• Coefficient de répartition fixe : $b_{i}=0$ et
  ${k_{a}}^{b_{i}}k_{i}=k_{i}$
• Coefficient de répartition ajustable : $b_{i}=1$ et
  ${k_{a}}^{b_{i}}k_{i}=k_{a}k_{i}$

Si on simplifie l’écriture de
l’équation de conservation de la masse au nœud en assimilant les débits aux biefs et aux prises sous forme de débits entrants $Q_{i}>0$ et de débits
sortants $Q_{i}<0$ , on obtient :

$\sum _{Q_{i}>0}C_{i}Q_{i}+C_{\mathit{nd}}\left[\sum _{Q_{i}<0,b_{i}=0}k_{i}Q_{i}+k_{a}\sum _{Q_{i}<0,b_{i}=1}k_{i}Q_{i}\right]=0$ et donc
$k_{a}=-{\frac{\frac{1}{C_{\mathit{nd}}}\sum _{Q_{i}>0}C_{i}Q_{i}+\sum _{Q_{i}<0,b_{i}=0}k_{i}Q_{i}}{\sum _{Q_{i}<0,b_{i}=1}k_{i}Q_{i}}}$

Or pour un nœud sans casier, la concentration au nœud peut
s’écrire :

$C_{\mathit{nd}}=\frac{\sum _{Q_{i}>0}C_{i}Q_{i}}{\sum _{Q_{i}>0}Q_{i}}$

L’équation de $k_{a}$ devient :
$k_{a}=-{\frac{\sum _{Q_{i}>0}Q_{i}+\sum _{Q_{i}<0,b_{i}=0}k_{i}Q_{i}}{\sum _{Q_{i}<0,b_{i}=1}k_{i}Q_{i}}}$

L’équation complète du calcul de $k_{a}$ donne :

$k_{a}=-{\frac{\left(\sum _{s_{b}Q_{b}>0}s_{b}Q_{b}+\sum _{Q_{p}>0}Q_{p}\right)+\left(\sum _{s_{b}Q_{b}<0,b_{b}=0}k_{b}s_{b}Q_{b}+\sum _{Q_{p}<0,b_{p}=0}k_{p}Q_{p}\right)}{\sum _{s_{b}Q_{b}<0,b_{b}=1}k_{b}s_{b}Q_{b}+\sum _{Q_{p}<0,b_{p}=1}k_{p}Q_{p}}}$

L’équation de conservation de la masse au nœud devient alors :

$\sum _{s_{b}Q_{b}>0}C_{b}s_{b}Q_{b}+\sum _{Q_{p}>0}C_{p}Q_{p}+C_{\mathit{nd}}\left(\sum _{s_{b}Q_{b}<0}{k_{a}}^{b_{b}}k_{b}s_{b}Q_{b}+\sum _{Q_{p}<0}{k_{a}}^{b_{p}}k_{p}Q_{p}\right)=0$

Afin d’éviter de placer trop
d’exponentielles qui pourraient pénaliser lourdement
les calculs, on pourra aussi l’écrire
cette équation de cette façon :

$\sum _{s_{b}Q_{b}>0}C_{b}s_{b}Q_{b}+\sum _{Q_{p}>0}C_{p}Q_{p}$
$+C_{\mathit{nd}}\left[\sum _{s_{b}Q_{b}<0,b_{b}=0}k_{b}s_{b}Q_{b}+\sum _{Q_{p}<0,b_{p}=0}k_{p}Q_{p}+k_{a}\left(\sum _{s_{b}Q_{b}<0,b_{b}=1}k_{b}s_{b}Q_{b}+\sum _{Q_{p}<0,b_{p}=1}k_{p}Q_{p}\right)\right]=0$